中学3年生《1月実力テスト・数学》問題＆解答・解説｜冬休み明けの総復習に！【無料】

冬休みが終わるとすぐに待っている「1月実力テスト」。特に数学は、計算力だけでなく、関数・図形・確率など幅広い単元を総合的に問われる重要な科目です。本記事では、中学校3年生向けに 冬休み明け1月実力テスト《数学》の無料問題と、ていねいな解答・解説 を収録しています。

入試でもよく出題される基礎〜応用の問題を厳選し、方程式、関数、相似、証明、資料の活用まで幅広く対策可能。冬休みの成果確認や、弱点克服、本番前の仕上げに最適です。確実に得点できる力をここで固めましょう。

【問題】数学の予想テストの問題

【問1】次の問いに答えなさい。
四則計算(1）−8+7+(−3)　を計算しなさい。

乗除計算(2)(−8ab)×3ab²を計算しなさい。

展開公式(3)(4−2)/5−(+5)/3を計算しなさい。

等式変形(4)=2(+)をｃについて解きなさい。

一次関数(5)変化の割合が2で、点(3,4）を通る一次関数の式を求めなさい。

方程式(6)3−2=24 と=10−4の連立方程式を解きなさい。

角度(7)正十角形の1つの内角の大きさを求めなさい。

球(8)半径が4cmの球の体積を求めなさい。

相対度数(9)ある中学校の生徒40人の通学時間を調べたところ階級値が14分の生徒が10人いた。この階級の相対度数を求めよ。

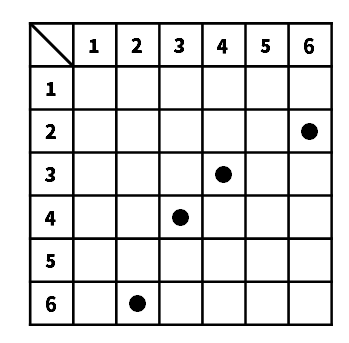
確率(10)大小2つのさいころを同時に投げるとき、出る目の数の積が12になる確率を求めなさい。

余事象（11）袋の中に、赤玉が3個、白玉が2個、合わせて5個の玉が入っている。この袋の中から同時に2個取り出すとき、少なくとも1個は白玉である確率を求めよ。

おうぎ形（12）弧の長さが6cm、半径が3cmのおうぎ形の面積を求めなさい。

二次関数（13）物を落とすとき、落ち始めてからｘ秒間に落ちる距離をｙｍとすると、ｙはｘの2乗に比例し、落ち始めてから3秒間に落ちる距離はおよそ45ｍであるとき、落ち始めてから2秒間には、何ｍ落ちるか求めなさい。

中央値（14）ある中学校の生徒8人の通学時間を調べると下の調査結果となった。この8人の通学時間の中央値を求めよ。
調査結果【　6分　9分　3分　4分　5分　9分　7分　13分　】

変化の割合（15）関数y＝ax²についてxの値が1から3まで増加するときの変化の割合が2であった。このときaの値を求めなさい。

【問2】
東西に延びている線路があり，途中には長さ800ｍのトンネルがある。毎日同じころに，貨物列車が西から東へ一定の速さで通るので，Aさん，Bさん，Cさんは，列車の速さと長さを知りたいと考えた。3人がそれぞれの場所で調べた内容と結果は，下のとおりである。この結果をもとに，貨物列車の速さを毎秒xm、長さをtmとして方程式をつくり，列車の速さと長さを求めなさい。

＜結果＞
Aさん 列車の先端から最後尾までが目の前を通過するのに要した時間12秒間
Bさん 列車の最後尾がトンネルに入った時刻：午後4時1分45秒
Cさん 列車の先端がトンネルから出た時刻：午後4時2分53秒

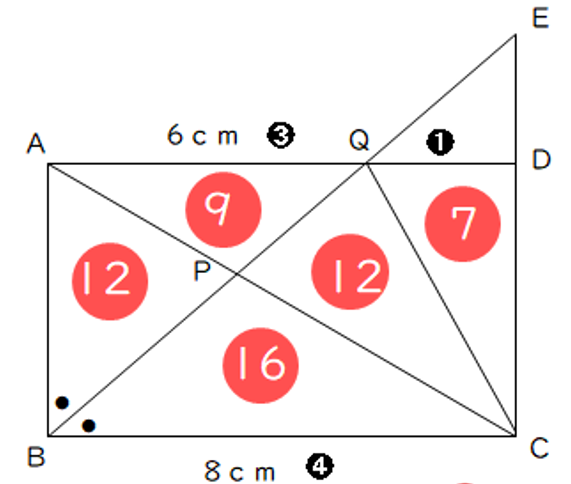
【問3】図のように。AB＝6ｃｍ、BC＝8ｃｍの長方形ABCDがあり、∠Bの二等分線とCDの延長との交点をEとする。また、BEとAC,ADとの交点をそれぞれP,Qとする。このとき、次の問いに答えなさい。

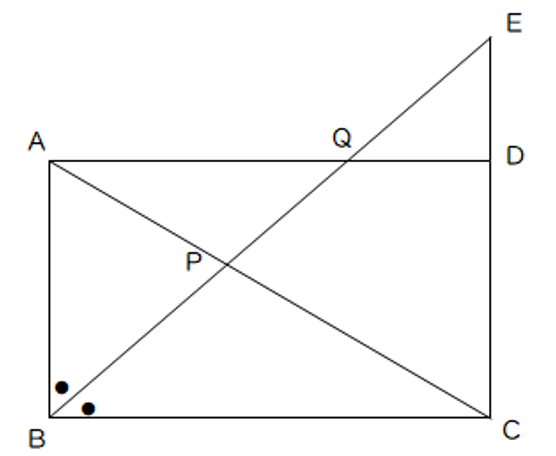
（1）EDの長さをそれぞれ求めよ。
（2）CPの長さをそれぞれ求めよ。
（3）四角形PQDCと三角形APBの面積比を求めよ。

【問4】次の図のように、母線の長さＯＡ＝15ｃｍ、底面の直径ＡＢ＝10ｃｍの円すいがある。このとき、次の問いに答えよ。

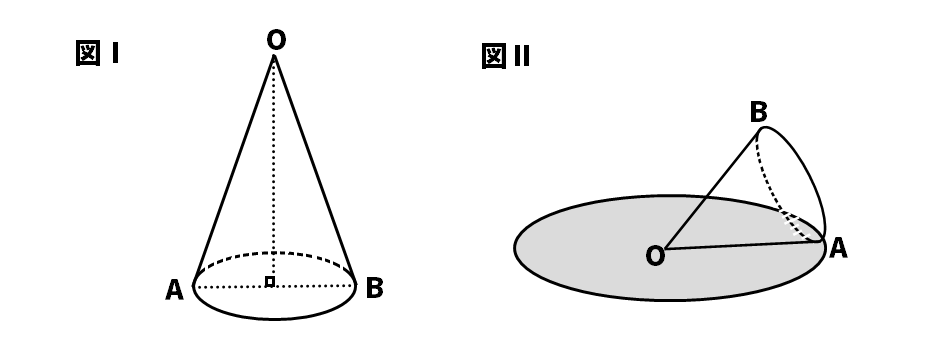
（1）図Ⅰの円すいの高さを求めよ。

（2）図Ⅰの円すいの側面を平面上に展開したときにできるおうぎ形の面積を求めよ。

（3）図Ⅱのように、図Ⅰの円すいの側面を平面上に置き、頂点Ｏを中心として、すべらないように転がす。このとき、点Ａがはじめて元の位置にもどるのは何回転したときか。

【解答】数学の予想テストの解答・解説

【問1】
（1）-8

（2）-24a²b³

（3）(7x-31y)/15 （15分の7x-31y)

（4）c=a/2-b

（5）y=2x-2

（6）(x,y)=(4,-6)

（7）144°

（8）256/3πcm³ (3分の256π)

（9）0.25

（10）1/9

（11）7/10

（12）92cm²

（13）20m

（14）6.5

（15）a=1/2

【問2】
y＝12x
68x＝800－y
これを解くと、x＝10　y＝120
これは問題に合う。

毎秒10ｍ　長さ120ｍ

【問3】
＜ポイント＞
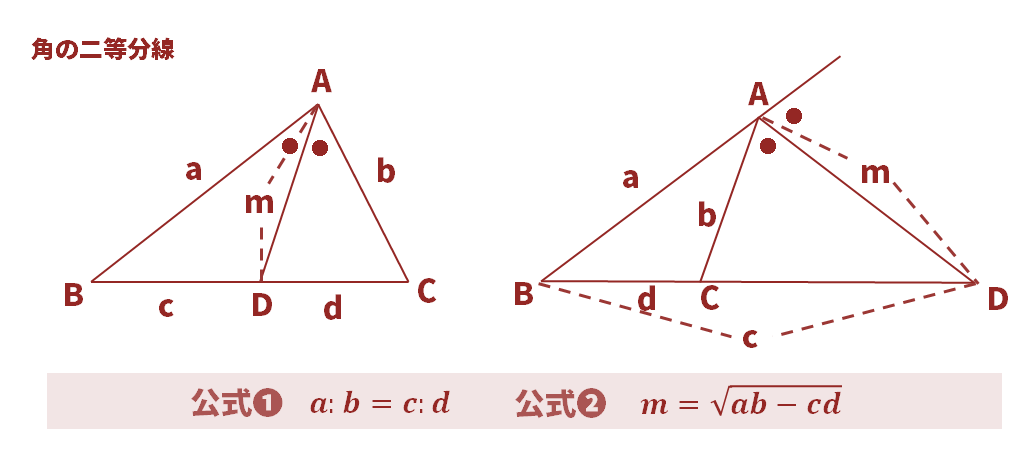
➊特に入試や実力テストでは「角を二等分する」、「二等分された角」などとあれば、角の二等分線定理を利用することが圧倒的に多い。
➋角の二等分線定理で単独で出題されることは少なく、合わせて相似や三平方の定理を途中組み合わせたり、使用させたりして解答させる。

（1）EDの長さ

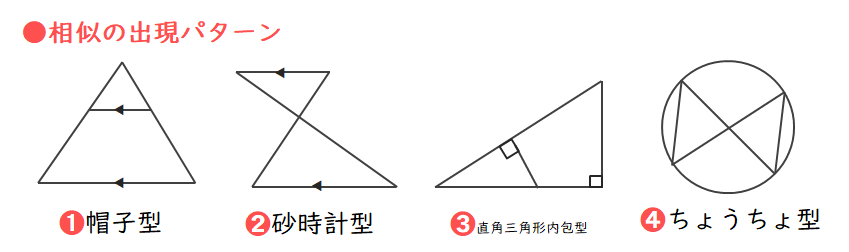
上の図の「相似の出現パターンの砂時計型」より、△AQB∽△DQEより、AB：DE＝AQ：QDが成り立つので、DE＝ｘとすると、6：ｘ＝6：2より、ｘ＝2ｃｍとなる。

（2）CPの長さ

ACは、三平方の定理より、10ｃｍ。また、角の二等分線定理より、AP：AC＝3：4よって、求めるCP=10×（4/7）となり、40/7ｃｍ

（3）四角形PQDCと三角形APBの面積比

相似比の2乗は面積比を利用すると、四角形PQDC：三角形APB＝19：12となる。

【解答】
（1）EDの長さ　2ｃｍ
（2）CPの長さ　40/7ｃｍ
（3）四角形PQDCと三角形APBの面積比　7：4

【問4】
（1）10√2cm
【解説】

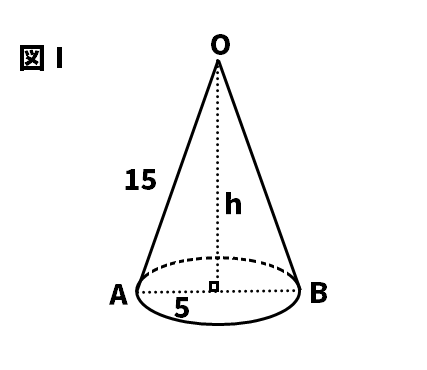
三平方の定理を利用して、求めましょう。

（2）75πcm²
【解説】円すいの側面を平面上に展開したときにできるおうぎ形の面積とは、元の円すいの側面積のことでしたね！
円すいの側面積の求め方＝母線×半径×π

（3）3回転
【解説】

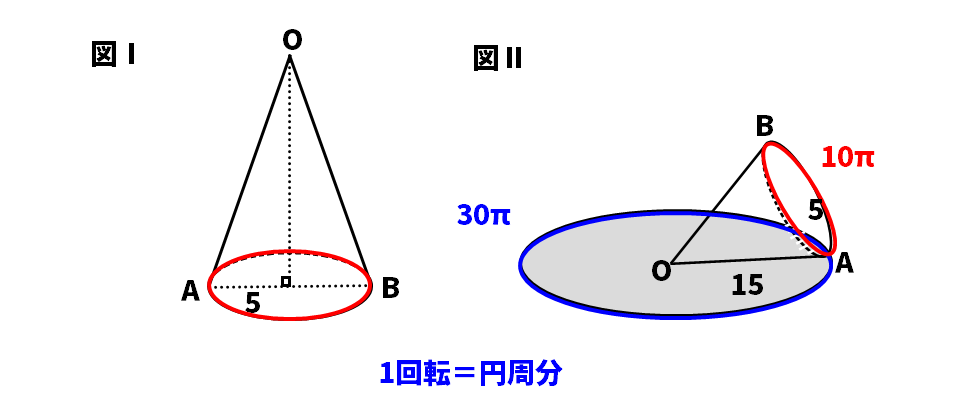
1回転は、円周の長さであるということが最大のポイントですね。今回は、図Ⅰの円すいの円周の長さが10πで図Ⅱの円すいの円周の長さが30π。30π÷10π＝3（回転）ということになります！