【高校入試数学】予想問題総まとめテスト｜中学3年間の重要ポイントを徹底確認

高校入試に向けて、数学の総仕上げをしたい受験生必見！本記事では、中学1年から3年までの重要単元を網羅した予想問題をまとめています。定期テストや過去問でよく出題されるポイントを中心に、効率よく復習できる構成になっています。苦手分野の確認や実力チェックにぜひ活用してください。

【高校入試数学】予想問題総まとめテスト

【問1】小問集合

【問2】方程式文章題
A,B2種類の砂糖水があります。Aの砂糖水100gとBの砂糖水200gを混ぜると15%の砂糖水になり,Aの砂糖水400gとBの砂糖水100gを混ぜると8%の砂糖水になります。Aの砂糖水の濃度をx%,Bの砂糖水の濃度をy%として,次の問いに答えなさい。

1 15%の砂糖水ができるときの砂糖の量の関係から方程式をつくりなさい。
2 8%の砂糖水ができるときの砂糖の量の関係から方程式をつくりなさい。
3 砂糖水Aと砂糖水Bのそれぞれの濃度を求めなさい。

【問3】関数
図のように、関数y=1/4ｘ²のグラフ上に2点A、Bがある。A、Bのy座標はどちらも1で、Aのx座標はBのx座標より小さくなっている。また、点Cが軸上にあり、y 座標は-3である。次の問いに答えなさい。

(1)点Aのx座標を求めなさい。

(2)△ABCで、辺BCを底辺とするときの高さを求めなさい。

【問4】平面図形
図のように、AB=4cm,CA=2cm,∠A=90°の直角三角形ABCがある。辺ABの中点をDとし、辺ABの垂直二等分線と∠Aの二等分線との交点をEとする。線分DEと辺BCとの交点をF、線分AEと辺BCとの交点をGとし、次の問いに答えよ。

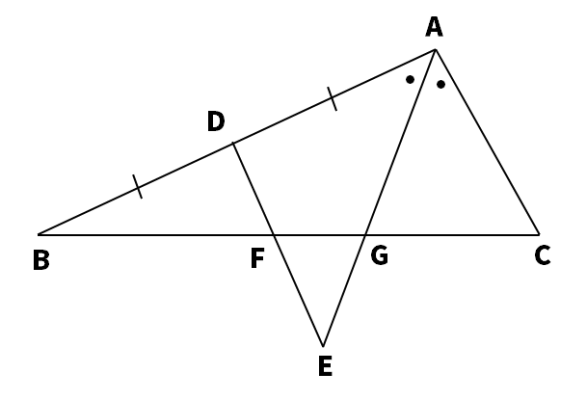
(1) 線分DFの長さを求めよ。

(2) △ADEの面積を求めよ。

(3) △ACG∽△EFG であることを証明せよ。

(4) 線分AGの長さを求めよ。

【問5】空間図形
下の図の円錐について、次の問いに答えなさい。

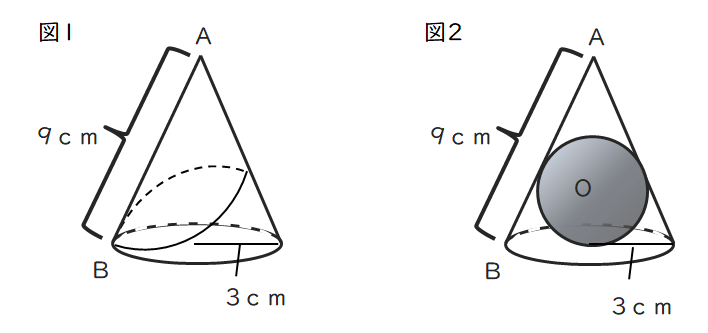
（1）図1の円錐の体積を求めよ。

（2）図1の円錐で、点Bから円錐の側面にそって一周し、点Bにもどる曲線をひく。この曲線がもっとも短くなるときの長さを求めよ。

（3）図2のように、この円錐にちょうど入る大きさの球Oがある。球Oの半径を求めよ。

【高校入試数学】予想問題総まとめテストの解答

【問1】
（1）1
（2）3a+2
（3）-3
（4）-3√5
（5）ｘ＝-5 ｙ＝-1
（6）3x(2y-3)
（7）y=8
（8）3
（9）0.1
（10）39

【問2】
1 x/100×100+y/100×200＝15/100×300
2 x/100×400+y/100×100＝8/100×500
3 砂糖水Aの濃度 5%, 砂糖水Bの濃度 20%

【問3】
（1）-2

（2）
A(-2, 1), B(2, 1), C(0, -3) だから、
△ABC=1/2×{2-(-2)}×{1-(-3)}=8

線分 BC の長さは、
三平方の定理の利用により、2√5

求める高さをhとすると
1/2 ×2√5×h=8
h=8√5/5

8√5/5　5分の8ルート5

二次関数と三平方の定理の融合問題は、一見難しそうに感じますが、問題のパターンや解き方の流れを理解すれば確実に得点できる分野です。グラフの読み取り、座標の設定、三角形の辺の長さを求める手順を一つずつ丁寧にこなすことが大切です。今回紹介した解法やポイントを繰り返し練習して、入試本番でも落ち着いて解けるようにしておきましょう。地道な積み重ねが、数学の応用力アップにつながります！

【問4】
(1) 1cm
△ABCで, 点Dは辺ABの中点,DF//ACより
BD:BA=DF:AC
1:2=DF:2
DF=1(cm)

(2) 2cm²

(3) △ACGと△EFG
対頂角は等しいから。∠AGC=∠EGF…➀
∠BAC=∠BDE=90°より。AC//FE
平行線の錯角は等しいので、∠CAG=∠FEG…➁
➀,➁より、2組の角がそれぞれ等しいから
∠ACG∽∠EFG

(4)4√2/3cm
△ADEは直角二等辺三角形だから,
AE=√2 AD=2√2 (cm) FE=2-1-1 (cm)
FE//AC, EG: AG=FE: CA=1:2だから
AG=2/3AE=2/3×2√2=4√2/3

【問4】
●今回使う公式（三角形に内接する円の半径の長さの求め方）

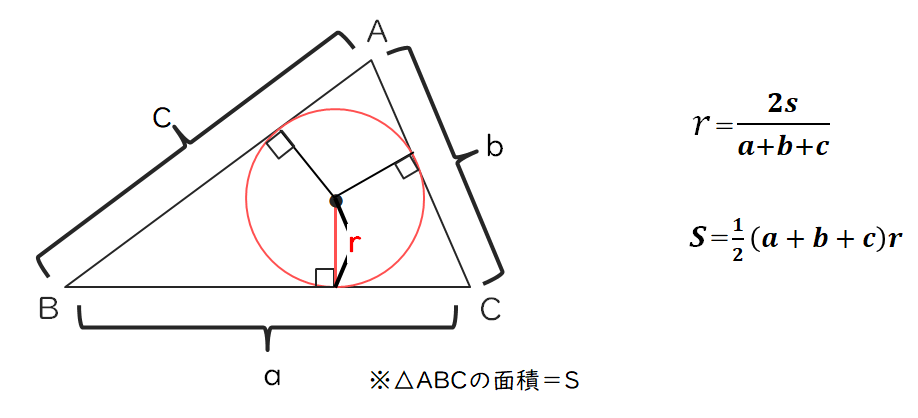
＜解説＞
（1）高さがわからないので、垂線を下ろして、三平方の定理を使う。そうすると6√2が高さとなる。よって、体積は3×3×π×6√2÷3＝18√2π

（2）円錐を展開して、BとB’を結んだ直線を求める。まず、中心角を求めることが解法の最初の手順。中心角は、120°。あとは、特別な直角三角形を使って、求めていくと、9√3となる。

（3）三角形に内接する円の半径の長さの求め方の公式を使うと、求める半径＝（2×△の面積）/（9+6+9）になる。
ここで、△の面積は、6×6√2÷2＝18√2なので、　36√2÷24＝3√2/2が答えとなる。

＜解答＞
（1）18√2ｃｍ²
（2）9√3ｃｍ
（3）3√2/2ｃｍ